Bildverstehen
Grundlagen Bilderkennung und Bildverstehen.
Definition
...ist eines der kompliziertesten informatischen Gebiete. Bildverarbeitung und Bildverstehen stehen eng beieinander. Dabei ist das Bildverstehen eher der künstlichen Intelligenz zuzuordnen. Bildverstehen ist ein Prozess, welcher als Ausgabe eine Folge von Beschreibungen ausgibt. Diese hängen natürlich extrem vom Bild und der dazugehörigen Fragestellung ab.
Bildverstehen ist die Rekonstruktion und Deutung einer Szene anhand von Bildern, so dass mindestens eine der folgenden operationalen Leistungen erbracht werden kann:
- Ausgabe einer verbalen Szenenbeschreibung
- Beantwortung verbaler Anfragen an das System
- navigieren von Robotern in der Szene
- planmäßiges Greifen und Manipulieren von Objekten der Szene
- Ausgabe von Warnsignalen bei gefährlichen Situationen
Grundbegriffe
Das Systemmodell nach Marr
Bild < primiäre Skizze < 2 1/2D Skizze < 3D-Modellrepräsentation
| Bild | digitales Rasterbild mit radiometrischen Eigenschaften jedes Bildpunktes |
|---|---|
| primäre Skizze | erster Eindruck - Datenmenge sinnvoll auf Wesentliche reduzieren |
| 2 1/2 D Skizze | Geometrische und photometrische Eigenschaften der Oberfläche, wie Tiefeninformation, Konturen oder Normalvektoren,partielle Form- und Geomiekonstruktion |
| 3D-Modell | Integration mehrerer 2 1/2 D Skizzen, Zerlegung in verallgemeinerte Zylinder, Aussagen über verdeckte Teile, Szenenbeschreibung |
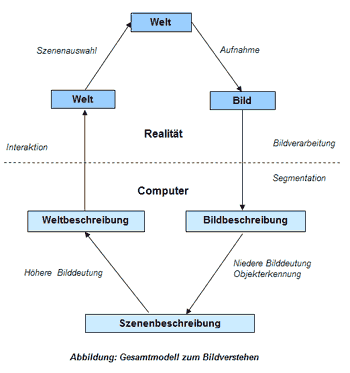
Repräsentationsebenen
| Welt | phyikalische Objekte mit Attributen, Objektkonfiguration, Bewegung der Objekte |
|---|---|
| Szene | 3D Ausschnitt der Welt und bestimmter Zeitpunkt |
| Bild | 2D Abbild einer Szene |
| Bildbeschreibung | Bottum-up, 2D Bildelemente |
| Szenenbeschreibung | Interpretation der Szenenelemente |
| Weltbeschreibung | Top - down mit Vorwissen |
Bildvorbereitung
...ist Grundlage zur Merkmalsextraktion und Bildsegmentierung. Es sollen Fehler im Bild korrigiert oder das Bild aufbereitet bzw. verbessert werden.
Dabei gibt es Punktoperationen, lokale Operationen und globale Operationen. Bei lokalen Operationen wird immer nur ein Teilbereich betrachtet, welcher meistens quadratisch gewählt wird. Dagegen ist bei globalen Operationen ein Ausgabebildpunkt von allen Eingangsbildpunkten, sprich den ganzen Originalbild, abhängig.
Punktoperationen
| Dehnung der Grauskala | Multipikation einer Kontrast-und Addition einer Helligkeitskonstante (+/-), damit Invertierung) |
|---|---|
| Lineare Dehnung der Grauskala | Die Grauskala wird via Kontrast und Helligkeit so modifiziert, dass das ganze Spektrum ausgenutzt wird. |
| Binarisierung/Schwellwertbildung | Trennen von bestimmten Objekten vom Hintergrund |
| Farbtransformation | die drei Farbauszüge R,G,B werden modifiziert |
| Hintergrundsubtraktion | es wird ein zweites Bild, wo nur der Hintergrund aufgenommen wurde, subtrahiert) |
| Masikierung | Extraktion semantisch bedeutsamer Bildteile durch eine Bitmaske) |
| Geometrische Transformation | bei Vergleich unterschiedlich großer Bilder Ortskoordinatentransformation o.ä. |
lokale Operationen
Lineare Faltung
Mit der Faltung lassen sich eine Vielzahl von Filtern (Hoch- und Tiefpassfilter) realisieren. Dabei wird ein LxM große Matrix benutzt, um den aktuellen Bildpunkt in Abhängigkeit von den umliegenden Punkten zu berechnen.
Die lineare Faltung berechnet die Werte des Ausgangsbildes aus einer rechteckigen (die Matrix H) Umgebung des Eingangsbildes. Die Eigenschaften der Faltungsoperation werden durch den Faltungskern (die Matrix H) bestimmt
Zeilen und Spalten der Matrix sind in der Bildverarbeitung immer kleiner als die des Eingangsbildes. Ausserhalb des Eingangsbildes liegende Punkte werden nach verschiedenen Verfahren gefüllt (Bereich ja für Matrixoperation notwendig)
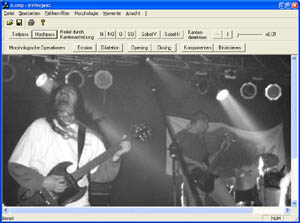
Eingangsbild Graustufe
Mittelwertoperator (Tiefpaßfilter)
3x3 Matrix mit 1/9 gefüllt zur Glättung der Grauwerte.. verstärkt tiefe Ortsfrequenzen und unterdrückt hohe. Somit verschinden kleine Grauwertspizen. Gleichmäßig helle Bildteile bleiben unverändert, Kanten werden aber verwischt. Es kann mit diesem Operator das Rauschen verringert werden. Dabei gehen aber andere relevante Informationen verloren.
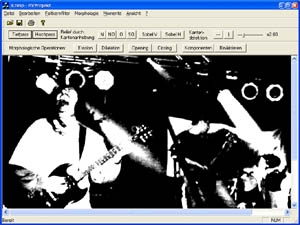
Ausgangsbild durch Tiefpassfilter
Laplace Operator (Hochpaßfilter)
Der Laplace hebt Grauwertdifferenzen hervor und dient zur Kantenhervorhebung). Er unterdrückt tiefe Ortsfrequenzen und hebt hohe hervor. Dadurch verschwinden gleichmäßig helle Bildanteile. Kanten werden somit betont.
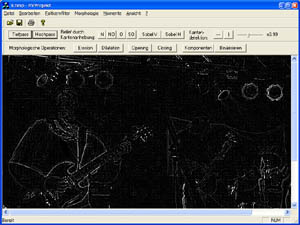
Ausgangsbild durch Hochpassfilter
Anhebung von Kanten in eine Vorzugsrichtung
.. durch je eine Faltungsmatrix für N,S,NO und SO-Richtung
Sobeloperator
Differenzbildung je zur übernächsten Zeile, um kleine Störungen zu umgehen.
...kleine Störungen benachbarter Zeilen / Spalten gehen nicht in das Ergebnis ein. Der Sobeloperator dient auch zur Kantenhervorhebung.
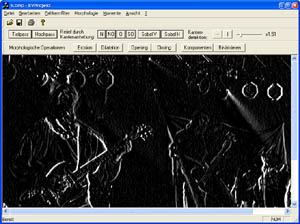
Gradient
Der Gradient ist ein weiteres Maß für die Uneinheitlichkeit in der lokalen Grauwertverteilung. Der Gradient-Operator ist eine Formel, welche eine Faltungsmatrix (z.B. einen Soebeloperator) einbezieht. Der Gradientoperator ist somit ein richtungsunabhängiger Operator, welcher aber nicht linear ist.
Rangfolgeoperationen
Rangfolgeoperationen basieren darauf, daß die N Bildpunkte in einer vorgegebenen lokalen Umgebung zu einem Bildpunkt in Abhängigkeit von ihrem Grauwert sortiert werden.
Minimaloperation
Entfernt Spitzen hoher Grauwerte und unschaft zu machen, aber vergrößert Flecken niederer Grauewerte)
Maximaloperation
Entfernt kleine Flecken niedriger Grauwerte, aber vergrößert Spitzen hoher Grauwerte
Medianoperation
Enfernt punktförmige Gebilde ohne unscharf zu machen, es entstehen keine neunen Grauwerte, dünne Linien können verschwinden)
globale Operationen
Um ein Problem zu lösen, ist es manchmal notwendig ein mathematisches Objekt in ein anderes Objekt zu transformieren und verwandtes Problem an diesem neu transformierten Objekt zu lösen. Dies wird im Besonderen in der Bildvererarbeitung genutzt, da es verschiedene Ansätze gibt, nach denen Berechnungen, um ein vielfaches einfacher werden.(Diskrete 2D-Fouriertransformation)
Mathematische Morphologie (Lehre der Form)
Beispielbild für die Erosion und Dilatation
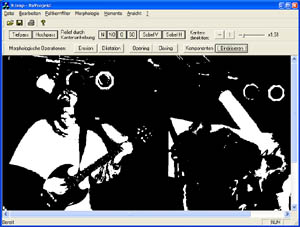
Eingangsbild ist das binarisiertes Ursprungsbild (Schwellwertbildung)
Jedes Rasterbild ist als Teilmenge von Z^n darstellbar. Binärbilder werden als Teilmengen von Z^2, bestehend aus Ortskoordinaten der Bildpunkte beschrieben. Dagegen werden Grauwert- oder zeitinvariante Binärbilder in Z^3 aus Ortskoordinaten und der Zeit bzw. dem Grauwert gebildet. Viele komplexe Bildverarbeitungsalgorithmen lassen sich auf folgende elementare Operationen zurückfühen.
Dilatation (X+B)
Die Dilatation fügt einem Bild X ein Strukturelement B zu. Deshalb ist es auch eine Bildverstärkende bzw. Bildverdickende Operation. Es ist möglich Teilchengruppen zu vereinigen, Löcher zu füllen oder Risse zu schliessen. Eine sehr einfache Art der Kantendetektion ist (X+B)\X.
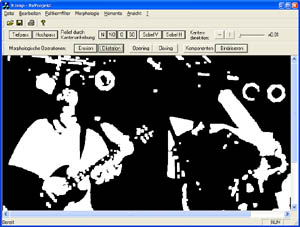
Bild nach Mehrfachanwendung der Dilatation (Beachte die Pixelzunahme)
Erosion (X-B)
Die Erosion ist das Gegenstück der Dilatation und entfernt die passenden Bildpunkte. Die Erosion vermindert somit die Bilddaten.
Anders gesagt, findet die Erosion Bildpunkte, die mit einem speziellem Muster von Elementen umgeben sind. Bei de Erosion werden schmale Stellen und kleine Objekte, deren Größe kleiner als die des Strukturelementes B ist, vollständig eliminiert. Die Erosion dient auch zur Kantenfindung.
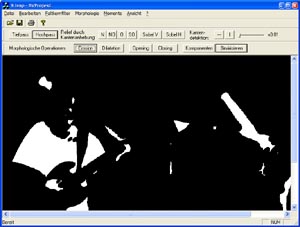
Bild nach Mehrfachanwendung der Erosion (man beachte die Pixelminderung)
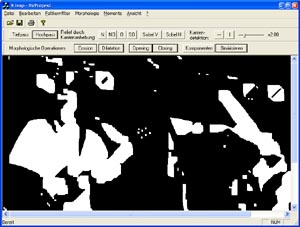
Mehrfach angewandtes Closing (Beachte verschwundenen Gitarrenhals)
Von diesen beiden Operationen werden das Opening ((X-B)+B) und das Closing ((X+B)-B) abgeleitet. Dabei bewirkt das Opening eine Eliminierung von im Verhältnis zum Strukturelement B kleinen Teilmengen des Bildes X. D.h. schmale Verbindungen oder auch alleinstehende Mengenelemente werden gelöscht. Dagegen werden beim Closing kleine Einschnitte und Zwischenräume geschlössen.
Anwendungen
- Alles oder nichts - Transformation(XxB)
- Abmagerung bzw. Skelletierung (X / (XxB))
- Verdickung
Dies sind iterierende Operationen, bei denen die gleiche Operation mit mehreren Strukturelementen hintereinander angewendet wird.b
Bildsegmentierung
Einleitung
Segmentierung bedeuted, das Bild in sinnvolle Bildteile aufzuteilen. Ziele der Segmentierung sind unter anderem
- Auffinden von Segmentierungsobjekten (Objekte mit homogenen Eigenschaften)
- Affinden von Segmentgrenzen (unterschiedlich helle Grauwertbereiche so unterscheidbar)
Arten von Segmentierung
- punktorientierte Verfahren (durch einfache Schwellwertoperationen wird Vordergrund getrennt)
- kantenorientierte Verfahren
- regionenorientierte Verfahren
- regelbasierte Verfahren (hier ist die Segmentform vorher bekannt)
Punktorientierte Segmentierung
Die einfachste Form der Segmentierung ist das Schwellwertverfahren. Ein Bildpunkt des Ausgangabildes wird auf 1 gesetzt, falls der Bildpunkt des Eingangsbildes einen bestimmten Wert übersteigt. Im Histogramm erkennt man oft ein oder mehrere Extremwerte. Zwischen den Extremwerten liegen die sinnvollsten Schwellwerte, da die lokalen Minima die Stellen darstellen, welche Vorder- und Hintergrund voneinander trennen. Da bei den meisten Bildern aber viele Extremwerte (multimodale Histogramme) sichtbar werden, treten natürlich Überschneidungen auf. Deshalb reicht die Schwellwertbildung auch nur in den seltesten Fällen für eine akzeptable Segmentation aus.
Mathematische Grundlagen der Bildsegmentierung
Nachbarschaftsrelationen
- 4 - Nachbarschaft (Nord,Süd,West,Ost)
- Diagonalnachbarschaft (Nordsüd,Südwest,Nordwest,Südost)
- 8 - Nachbarschaft (4 - Nachbarschaft und Diagonalnachbarschaft), also alle benachtbarten Punkte)
- Nachbarschaft im Hexagonalraster (Kreise und Linien hier besser darstellbar)
Zwei Punkte sind verbunden, wenn es einen Weg zwischen diesen gibt. Eine nichtleere Teilmenge einer Nachbarschaftsstruktur heißt zusammenhängend (Gebiet, Region), falls zwei beliebige Punkte der Teilmenge miteinander verbunden sind.
Eine Menge von untereinander diskunkten Gebieten der Nachbarschaftsstruktur heißt Zerlegung, wenn die Vereinigung aller Gebiete wieder das Gesamtbild ergibt. Die durch die Verbundenheitsrelation erzeugten Äquivalenzklassen heissen Komponenten. Die Komponenten sind die maximal zusammenhängenden Teilmengen des Bildes.
Bestimmung von Komponenten
Ein Algorithmus errinnert an die Tiefensuche. Die Komponenten werden nacheinander gefunden. Ein anderer ist das Zeilenkoinzidenzverfahren.
Gebietsbasierte Segmentierung
Mit dem Region Growing Verfahren werden die Komponenten bestimmt. Es können mehrere Startpunkte (Saatzellen) i, Bild festgelegt werden, von denen ausgehend die Segmentierung erfolgen soll. Falls sich im Laufe des Algorithmus zwei Gebiete berühren sollte, wird das Homogenitätskriterium überprüft, um eventuell die Gebiete zu einem zu vereinigen.
Ein weiterer Ansatz ist der Split and Merge Algorithmus. Bei diesem Algorithmus wird in der Splitphase das Bild rekursiv solange in Teilgebiete zerlegt, bis jedes Teilgebiet das Homogenitätskriterium erfüllt. In der Merge Phase werden nun diejenigen Teilgebiete die das gleiche Homogenitätskriterium erfüllen und benachbart sind, zu einem Gebiet zusammengefasst.
Kantenorientierte Segmentierung
Das Ziel dieser Art der Segmentierung ist das Auffinden von Randkanten (Randwege oder Konturen) von Gebieten. Dazu gehören folgende Aufgaben:
- Kantendetektion (man erhält eine Menge Kantenverdächtiger Punkte)
- Kantenverdünnung / Skelettierung (die Menge wird zu einer eindimensionalen Menge vermindert)
- Kantenverfolgung (um gefundene Kanten zu verlängern oder zu schließen)
Ein Gebietsnachbarschaftsgraph zeigt in Form eines Graphen, wie die Segmente in welcher Hierachie im Bild liegen. Der Umgibtgraph zeigt dagegen wunderbar auf, welche Gebiete wie eingeschlossen sind.
Modellabhängige Segmentierung
- Matchen (vergleichen des Bildes mit einem Muster)
- Hough-Transformation (findet Geraden durch Angabe von Vektoren)
Merkmale von Objekten
Zur automatischen Erkennung von Bildern sind Verfahren notwendig, welche die Merkmal von Objekten extrahieren können. Diese Merkmale dienen zur charakteristischen Beschreibung von Objekten und der wesentlichen Unterstützung bei der Objekterkennung. Voraussetzung ist ein segmentiertes Bild, wo für einzelne Segmente die Merkmale berechnet werden können. Mit Hilfe der gewonnenen Merkmale will man die Segmente bestimmten Objekten zuordnen können. Um dies zu erreichen, sind zwei fast unvereinbare Kriterien notwendig:
- sie müssen berechenbar sein, d.h. auf konkreten Abbildungen von Objekten basieren
- sie müssen von Besonderheiten einer konkreten Abbbildung unabhängig sein, d.h. invariant bezüglich Verschiebung, Drehung, Dehnung, Perspektive, Beleuchtung oder Verdeckung
Geometrische Merkmale
- Fläche, Umfang, Länge, Breite
- Kompaktheit, Rundheit (Umfang hoch 2 durch 4PiFläche)
- Objektumschreibende oder einbeschriebene n-Ecke
- kleinstes umschreibendes achsenparalleles Rechteck (ferret box)
- umschreibendes Rechteck minimaler Fläche (Minimum bounding rectangle - MBR)
- Aspect Ratio (AR) - Verhältnis Höhe - Breite einer ferret box oder MBR als Logaritmus
- Füllungsgrad, gibt prozentual an wieviel Fläche im Rechteck mit dem Objekt ausgefüllt sind
- konvexe Hülle als Rechteck
- oktagonale Hülle läßt Stufen aus rechteckigen Winkel zu (ist somit achtseitig)
- konvexer Kern
Momente
...dienen zum Finden von invarianten Merkmalen. Momente erster Ordnung sind die Merkmale, die nicht translationsinvariant sind, d.h. die von der Position des Objektes im Bild abhängig sind.
Momente erster Ordnung
- Anzahl der Zeilen des Objektes
- Anzahl der Spalten des Objektes (werden benötigt um Objektschwerpunkt zu berechnen)
- Schwerpunktkoordinaten (Zeilen bzw. Spalten durch Fläche)
Zentrierte Moment(p,q) - ter Ordnung sind invariant gegenüber Translation. Das normierte zentrierte Moment(p,q) - ter Ordnung ist invariant gegenüber Ähnlichkeitstransformation.
Lauflängenkodierung
Ein Lauf ist ein Tripel (s,z,n), wobei S die Spalte, Z die Zeile und n die Länge eines zusammenhängenden Bereichs von horizontal aneinandergrenzenden Objektpunkten ist. Unter einer Lauflängenkodierung versteht man eine Menge von solchen Läufen. Mit Hilfe der Lauflängenkodierung lassen sich sehr einfach die Momente berechnen.
Eulerzahl
Die Eulerzahl E ist definiert durch E = B - L. B ist die Anzahl der Objekte und L die Anzahl an Löchern (Hintergrund, der von einem Objekt umgeben wird). Die Eulerzahl wird ermittelt, indem mehrere 2x2 Masken über das Bild geführt werden und die jeweiligen Trefferhäufigkeiten benutzt werden, um mit Hilfe einer Formel die Eulerzahl zu berechnen.
Relationalstrukturen
...erlauben eine Formbeschreibung auf der Basis lokaler Beschreibungselemente und Ihrer Beziehung untereinander und werden als Graphen dargestellt.
Mustererkennung
Ziel ist es, den durch Segmentierung gefundenen Objekten, Bedeutungen zuzuweisen. Dabei können einzelne Objekte, Gruppen oder auch Relationen zwischen Objekten die Grundlage sein. Das Grundprinzip ist einfach. Aus den berechnetet Objekten oder Gebieten werden Merkmale extrahiert, welche durch Training und bekanntes Wissen klassifiziert und mit einer bestimmten Bedeutung versehen werden.
Numerische Klassifikation
Ein Objekt wird durch einen Merkmalsvektor beschrieben. Bei einer numerischen Klassifikation wird jeder Vektor einer bestimmten Klasse K zugeordnet.
Lineare Klassifikation
Einordnung durch eine Entscheidungsfunktion
Abstandsklassifikatoren
Klassifizierung durch "geometrischen Abstand" des Objektes zu den Klassen Minimum - Distance - Klassifikator sowie Nearest - Neighbour - Klassifikator
statistische Klassifikation
Hier wird die Wahrscheinlichkeitsrechnung mit bedingten Wahrscheinlichkeiten genutzt. Ein Klassifikator aus dieser Gruppe ist der Maximum - Likelihood - Klassifikator.
Kontextabhängige Klassifikation
Ein Objekt wird hier nicht allein klassifiziert, sondern im Verbund bzw. im Kontext mit anderen Objekten. Somit findet hier eine Klassifikation von Strukturen (Graphen mit Objekten oder Kanten als Knoten und Nachbarschaftsrelationen) statt. Es gibt zwei Verfahren:
- Relaxation: Da die Vielfalt der möglichen Graphen groß ist, wird durch Iteration versucht, die Objekte so zu klassifizieren, dass die vorgegebenen Relationen erfüllt werden.
- Graph-Matching: Es gibt eine geringe Anzahl bekannter Graphen. Ein zu klassifizierender Graph wird einfach dem Ähnlichsten zugeordnet.
Diskrete Relaxation
Es wird von einer Segmentierung einer Nachbarschaftstruktur und einem Gebietsnachbarschaftsgraphen ausgegangen. Durch ein iteratives Verfahren wird versucht die Bedeutungen B sinnvoll unter Beachtung der Kanten zuzuordnen.
Kontinuierliche Relaxation
Hier wird jedem Objekt eine Wahrscheinlichkeit zugeordnet, die die Zugehörigkeit zu den entsprechenden Klassen spezifizieren soll. Im Folgenden wird iteriert und in jedem Durchgang diese Wahrscheinlichkeiten angepasst. Dabei werden die Nachbarobjekte betrachtet und überprüft, ob die Klassifizierung mit dem aktuellen Objekt kompatibel ist oder nicht. Sind die benachbarten Objekte kompatibel, so werden die entsprechenden Wahrscheinlichkeiten der Klassenzuweisungen erhöht. Sind sie inkompatibel, so werden die Wahrscheinlichkeiten verringert. Bei Erfüllung einer bestimmten Bedingung (Abbruchbedingung), wird die Iteration beendet.
Dreidimensionale Bildinterpretation
...ist die Gestaltsrekonstruktion dreidimensionaler Objekte. Grundlage sind visuelle Eingangsdaten von visuellen Sensoren (eine oder mehrere Kameras), die eine statische oder dynamische Szene abbilden.
- statische Szenen (Lichtänderungen möglich, aber keine Objektbewegungen während der Bildaufnahme)
- dynamische Szenen (Objektbewegungen während der Aufnahme möglich)
- statischer Bildaufnahme (Kameras sind fix und unbeweglich während der Aufnahme)
- dynamische Szenen (Kameras sind frei beweglich)
Generierung einer 2 1/2 D-Skizze
Diese Skizze ist ein wichtiger Zwischenschritt auf dem Weg zur Gestaltsrekonstruktion. Sie beschreibt eine unvollständige räumliche Information der sichtbaren Oberflächen eines Objektes. Für die Erstellung der Skizze gibt es verschiedene Vorgehensweisen. Einige sind eng an der meschlichen Wahrnehmung orientiert. Die meisten dieser Prinzipien kann man isoliert betrachten, hat sich der Begriff Shape from X (X steht für die jeweilige Methode) entwickelt.
Möglichkeiten der 2 1/2 D - Repräsentation
- Tiefenbilder (in jedem Pixel wird die Entfernung zur Kamera mit codiert)
- Surface Patches (zu jedem Pixel wird die Orientierung der Oberfläche codiert)
- Diskontinuitäten in der Entfernung (z.B. als Raumkurven)
- Approximation (von kontinuierlichen Oberflächen z.b. durch B-splines)
- Kombinationen der genannten Repräsentationsformen
Formale Präzisierung
Der Vektor zum aufzunehmenden Punkt ist der zu messende Szenenwert. Er wird über die dreidimensionale Umgebung des Sensors aufgenommen. Somit stellt dies eine Abbildung eines Vektors (x,y,z) in die reellen Zahlen dar. Szenenwerte können u.a. Grau- oder Farbwerte bei Kameras oder Entfernungen bei Lasern sein.
Eine optische Abbildung A ist vereinfacht nichts anderes als eine Projektion der Szene S auf ein Bild E, also E = A(S).
Probleme
Szenenobjekte sind nun anhand der Bilder wieder als dreidimensionale Körper darzustellen. So ist es notwendig die inverse Abbildung von A zu untersuchen. Eine eindeutige zuordnung ist aber i.a. nicht möglich. Aus diesem Grund ist das Problem beinahe immer nur eingeschränkt lösbar
- nur interessante und relevante Informationen der Szene werden betrachtet
- nur eine engere Wahl von Tiefenpunkten von Objekten (Tiefenanalyse)
Drei naheliegende Grenzen der Gestaltsrekonstruktion
- Ist nur für sichtbare Objektflächen möglich.
- Da die Objekte nicht immer aus allen Richtungen aufgenommen werden, ist meist nur eine 2 1/2 D Skizze möglich.
- Aufgrund der Bildrasterung und des Abstandes Kamera-Objekt ist die Ortsauflösung der Objektoberfläche eingeschränkt.
Shape from contour
Einführung
Beliebige dreidimensionale Objekte können anhand ihrer Konturen erkannt und lokalisiert werden. Voraussetzung dafür ist, dass ausreichend geometrische Modelle der Objekte vorhanden sind. Der Walz-Algorithmus versucht, zweidimensionale Linienzeichnungen dreidimensional zu interpretieren.
Die Linienzeichnung ist ein ungerichteter Graph, welche aus Knoten und Abschnitten besteht. Während der 3d-Interpretation werden den Knoten und Abschitten unterschiedliche Bedeutungen zugeordnet. (Markierung durch Marken an den jeweiligen Bildelementen)
Bildelemente mit Bedeutung können nicht wahllos zugeordnet werden. Es müssen dabei die bestehenden Relationen (physikalische Fakten) zwischen den Bedeutungen beachtet werden. Aufgabe ist es nun, konsistente Markierungen für eine 2d-Linienzeichnung zu finden oder wenigstens die Ausgangsmenge von Markierungen durch Entfernen der inkonsistenten Markierungen stark einzuschränken.
Annahmen
- keine Schatten oder Bruchlinien
- alle Eckpunkte sind Schnittpunkte von genau drei aufeinandertreffenden Flächen eines Objektes. Die obereren Eckpunkte von Pyramiden sind nicht gestattet.
- allg. Beobachtungspunkt, d.h. dass bei geringer Bewegung des Auges (bzw. Kamera) keine Schnittpunkte ihren Typ ändern
Kantenmarken
Es gibt vier Möglichkeiten:
- "-" konkave Kante mit zwei sichtbaren Flächen
- "+" konvexe Kante mit zwei sichtbaren Flächen
- "->" konvexe Kante mit einer sichtbaren Fläche in Pfeilrichtung (hier rechts)
- "<-" konvexe Kante mit einer sichtbaren Fläche in Pfeilrichtung (hier links)
Knotenmarken
Knoten können aufgrund der einlaufenden Kanten ebenfalls mit Marken versehen werden. Von der kombinatorischen Menge der theroretisch möglichen Anzahl ist aber nur ein geringer Teil (18) möglich.
Da an jedem Knoten genau drei Flächen zusammenstoßen, unterteilt ein Knoten den 3d-Raum in acht Oktanten. Stellt man sich nun ein,zwei.. oder sieben Oktanten ausgefüllt vor und und den Betrachter im freien Oktanten, dann erhält man alle möglichen Knotentypen. Der Fall das nur 2, 4 oder 6 Oktanten ausgefüllt sind, kann nicht eintreten.
Es gibt vier Knotentypen:- "<" L
- "Y" Gabel
- "->" Pfeil
- "T" T (nur bei partieller Überdeckung möglich)
Nun hat man aber noch nicht die Marken der Kanten berücksichtigt, die in den jeweiligen Knoten zusammenlaufen. Physikalisch sind von den rein kominatorisch Möglichen 208 nur 18 möglich.
Walz Algorithmus
Ziel: Finde für die Linienzeichnung eine Zuordnung der Marken und Knoten so, dass jeder Knoten eine zulässige Markierung im Sinne der 18 Möglichkeiten besitzt und die Marken der zusammengesetzten Kantenstücke übereistimmen.
Eine weitere Annahme soll sein, das jeder Gegenstand im Raum nur aufgehängt ist, d.h. die Hintergrundbegrenzungslinien sind nur Pfeilmarken.
Hinweise zur Markierung
- Es gibt nur eine Art Pfeil mit mit Pfeilmarken na der linken und rechten Kante. Für solch einen Pfeil muss die mittlere Kante mit einem "+" versehen werden.
- Es gibt nur eine Art Gabel mit irgendeinem "+". Für diese Gabel müssen alle Kanten mit "+" versehen werden.
Der Knotenmarkierungsalgorihmus Waltz
- Bilde eine Liste L mit allen Knoten (Schnittpunkten)
- Enferne solange, bis die Liste leer ist...
- das erste Element in der Liste. Nenne das Element "aktuellen Knoten"
- falls der aktuelle Knoten noch nicht aufgesucht wurde, erstelle für ihn eine Menge von Knotenmarken, die für den Knotentyp alle möglichen Marken enthält. Eine Mengenänderung hat somit stattgefunden.
- Wenn irgendeine Knotenmarke aus der Menge des aktuellen Knotens mit allen Knoten in der Menge irgendeines benachbarten Knotens nicht kompatibel ist, eliminiere diese inkompatible Marke aus der Menge des aktuellen Knotens. Eine Mengenänderung hat somit stattgefunden.
- Falls eine Mengenänderung stattfand, setze jeden benachbarten Knoten, der eine Markenmenge besitzt und nicht in der Liste L enthalten ist, an den Anfang der Liste L.
Ohne die Annahme, dass Objekte frei im Raum hängen, wären die Interpretationen nicht mehr eindeutig. Durch Einführen von Schatten können solche Mehrdeutigkeiten beseitigt werden. Dazu benötigt man aber weitere Kantenmarkierungen für die Schatten und Bruchlinien. Die Anzahl der zulässigen Markierungen erhöht sich dann aber sprunghaft!
Quellen
Quelle: Skript von Dr. Johannes Steinmüller an der Technischen Universität ChemnitzLinks
Das Programm habe ich geschrieben, um einige Filter ausprobieren zu können. Alle obigen Bilder sind Screenshots des Programms. Es dient zum ausprobieren. Eine kleine Textfile mit Hilfe wird beigelegt.